ParametricFunction#

Qualified name: manim.mobject.graphing.functions.ParametricFunction

class ParametricFunction(function, t_range=None, scaling=<manim.mobject.graphing.scale.LinearBase object>, dt=1e-08, discontinuities=None, use_smoothing=True, use_vectorized=False, **kwargs)[source]#

Bases: VMobject

A parametric curve.

Parameters:

  • function (Callable[[float, float], float]) – The function to be plotted in the form of (lambda x: x**2)

  • t_range (Sequence[float] | None) – Determines the length that the function spans. By default [0, 1]

  • scaling (_ScaleBase) – Scaling class applied to the points of the function. Default of LinearBase.

  • use_smoothing (bool) – Whether to interpolate between the points of the function after they have been created. (Will have odd behaviour with a low number of points)

  • use_vectorized (bool) – Whether to pass in the generated t value array to the function as [t_0, t_1, ...]. Only use this if your function supports it. Output should be a numpy array of shape [[x_0, x_1, ...], [y_0, y_1, ...], [z_0, z_1, ...]] but z can also be 0 if the Axes is 2D

  • discontinuities (Iterable[float] | None) – Values of t at which the function experiences discontinuity.

  • dt (float) – The left and right tolerance for the discontinuities.

Examples

Example: PlotParametricFunction

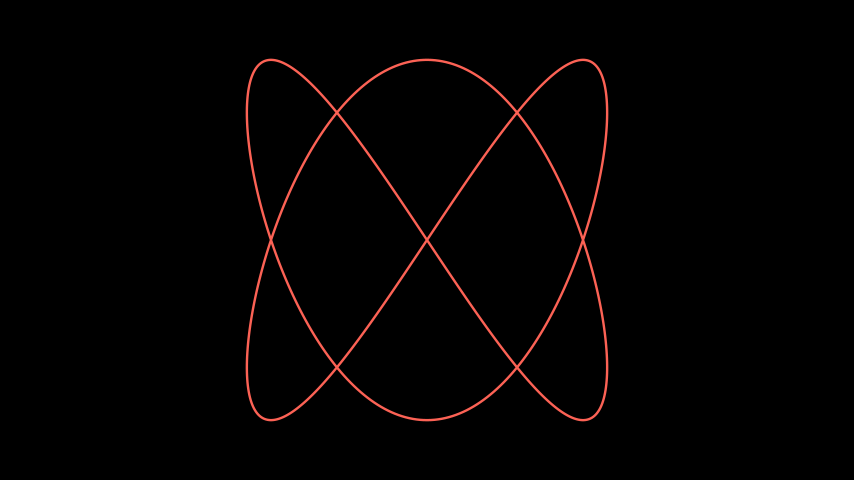
../_images/PlotParametricFunction-1.png 
from manim import *

class PlotParametricFunction(Scene):
    def func(self, t):
        return np.array((np.sin(2 * t), np.sin(3 * t), 0))

    def construct(self):
        func = ParametricFunction(self.func, t_range = np.array([0, TAU]), fill_opacity=0).set_color(RED)
        self.add(func.scale(3))

class PlotParametricFunction(Scene):
    def func(self, t):
        return np.array((np.sin(2 * t), np.sin(3 * t), 0))

    def construct(self):
        func = ParametricFunction(self.func, t_range = np.array([0, TAU]), fill_opacity=0).set_color(RED)
        self.add(func.scale(3))

Example: ThreeDParametricSpring

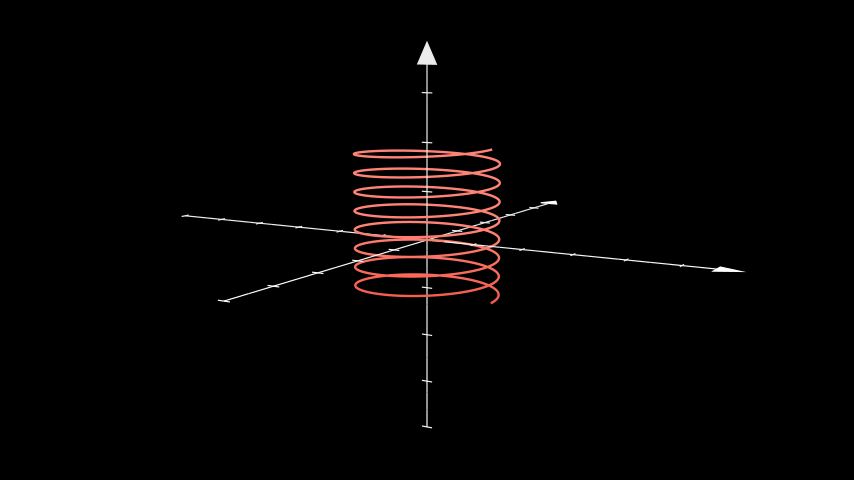
../_images/ThreeDParametricSpring-1.png 
from manim import *

class ThreeDParametricSpring(ThreeDScene):
    def construct(self):
        curve1 = ParametricFunction(
            lambda u: np.array([
                1.2 * np.cos(u),
                1.2 * np.sin(u),
                u * 0.05
            ]), color=RED, t_range = np.array([-3*TAU, 5*TAU, 0.01])
        ).set_shade_in_3d(True)
        axes = ThreeDAxes()
        self.add(axes, curve1)
        self.set_camera_orientation(phi=80 * DEGREES, theta=-60 * DEGREES)
        self.wait()

class ThreeDParametricSpring(ThreeDScene):
    def construct(self):
        curve1 = ParametricFunction(
            lambda u: np.array([
                1.2 * np.cos(u),
                1.2 * np.sin(u),
                u * 0.05
            ]), color=RED, t_range = np.array([-3*TAU, 5*TAU, 0.01])
        ).set_shade_in_3d(True)
        axes = ThreeDAxes()
        self.add(axes, curve1)
        self.set_camera_orientation(phi=80 * DEGREES, theta=-60 * DEGREES)
        self.wait()

Attention

If your function has discontinuities, you’ll have to specify the location of the discontinuities manually. See the following example for guidance.

Example: DiscontinuousExample

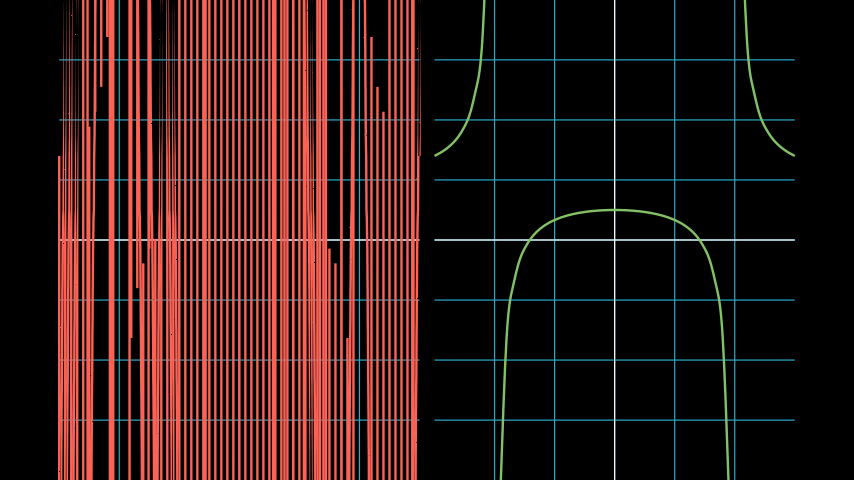
../_images/DiscontinuousExample-1.png 
from manim import *

class DiscontinuousExample(Scene):
    def construct(self):
        ax1 = NumberPlane((-3, 3), (-4, 4))
        ax2 = NumberPlane((-3, 3), (-4, 4))
        VGroup(ax1, ax2).arrange()
        discontinuous_function = lambda x: (x ** 2 - 2) / (x ** 2 - 4)
        incorrect = ax1.plot(discontinuous_function, color=RED)
        correct = ax2.plot(
            discontinuous_function,
            discontinuities=[-2, 2],  # discontinuous points
            dt=0.1,  # left and right tolerance of discontinuity
            color=GREEN,
        )
        self.add(ax1, ax2, incorrect, correct)

class DiscontinuousExample(Scene):
    def construct(self):
        ax1 = NumberPlane((-3, 3), (-4, 4))
        ax2 = NumberPlane((-3, 3), (-4, 4))
        VGroup(ax1, ax2).arrange()
        discontinuous_function = lambda x: (x ** 2 - 2) / (x ** 2 - 4)
        incorrect = ax1.plot(discontinuous_function, color=RED)
        correct = ax2.plot(
            discontinuous_function,
            discontinuities=[-2, 2],  # discontinuous points
            dt=0.1,  # left and right tolerance of discontinuity
            color=GREEN,
        )
        self.add(ax1, ax2, incorrect, correct)

Methods

generate_points

Initializes points and therefore the shape.

get_function

get_point_from_function

init_points

Initializes points and therefore the shape.

Attributes

animate

Used to animate the application of any method of self.

animation_overrides

color

depth

The depth of the mobject.

fill_color

If there are multiple colors (for gradient) this returns the first one

height

The height of the mobject.

n_points_per_curve

sheen_factor

stroke_color

width

The width of the mobject.
_original__init__(function, t_range=None, scaling=<manim.mobject.graphing.scale.LinearBase object>, dt=1e-08, discontinuities=None, use_smoothing=True, use_vectorized=False, **kwargs)#

Initialize self. See help(type(self)) for accurate signature.

Parameters:

  • function (Callable[[float, float], float]) –

  • t_range (Optional[Sequence[float]]) –

  • scaling (_ScaleBase) –

  • dt (float) –

  • discontinuities (Optional[Iterable[float]]) –

  • use_smoothing (bool) –

  • use_vectorized (bool) –

generate_points()[source]#

Initializes points and therefore the shape.

Gets called upon creation. This is an empty method that can be implemented by subclasses.

init_points()#

Initializes points and therefore the shape.

Gets called upon creation. This is an empty method that can be implemented by subclasses.