Graph

Qualified name: manim.mobject.graph.Graph

class Graph(vertices, edges, labels=False, label_fill_color=ManimColor('#000000'), layout='spring', layout_scale=2, layout_config=None, vertex_type=<class 'manim.mobject.geometry.arc.Dot'>, vertex_config=None, vertex_mobjects=None, edge_type=<class 'manim.mobject.geometry.line.Line'>, partitions=None, root_vertex=None, edge_config=None)

Bases: GenericGraph

An undirected graph (vertices connected with edges).

The graph comes with an updater which makes the edges stick to the vertices when moved around. See DiGraph for a version with directed edges.

See also

GenericGraph

Parameters:

• vertices (list[Hashable]) – A list of vertices. Must be hashable elements.

• edges (list[tuple[Hashable, Hashable]]) – A list of edges, specified as tuples (u, v) where both u and v are vertices. The vertex order is irrelevant.

• labels (bool | dict) – Controls whether or not vertices are labeled. If False (the default), the vertices are not labeled; if True they are labeled using their names (as specified in vertices) via MathTex. Alternatively, custom labels can be specified by passing a dictionary whose keys are the vertices, and whose values are the corresponding vertex labels (rendered via, e.g., Text or Tex).

• label_fill_color (str) – Sets the fill color of the default labels generated when labels is set to True. Has no effect for other values of labels.

• layout (str | dict) – Either one of "spring" (the default), "circular", "kamada_kawai", "planar", "random", "shell", "spectral", "spiral", "tree", and "partite" for automatic vertex positioning using networkx (see their documentation for more details), or a dictionary specifying a coordinate (value) for each vertex (key) for manual positioning.

• layout_config (dict | None) – Only for automatically generated layouts. A dictionary whose entries are passed as keyword arguments to the automatic layout algorithm specified via layout of networkx. The tree layout also accepts a special parameter vertex_spacing passed as a keyword argument inside the layout_config dictionary. Passing a tuple (space_x, space_y) as this argument overrides the value of layout_scale and ensures that vertices are arranged in a way such that the centers of siblings in the same layer are at least space_x units apart horizontally, and neighboring layers are spaced space_y units vertically.

• layout_scale (float | tuple) – The scale of automatically generated layouts: the vertices will be arranged such that the coordinates are located within the interval [-scale, scale]. Some layouts accept a tuple (scale_x, scale_y) causing the first coordinate to be in the interval [-scale_x, scale_x], and the second in [-scale_y, scale_y]. Default: 2.

• vertex_type (type[Mobject]) – The mobject class used for displaying vertices in the scene.

• vertex_config (dict | None) – Either a dictionary containing keyword arguments to be passed to the class specified via vertex_type, or a dictionary whose keys are the vertices, and whose values are dictionaries containing keyword arguments for the mobject related to the corresponding vertex.

• vertex_mobjects (dict | None) – A dictionary whose keys are the vertices, and whose values are mobjects to be used as vertices. Passing vertices here overrides all other configuration options for a vertex.

• edge_type (type[Mobject]) – The mobject class used for displaying edges in the scene.

• edge_config (dict | None) – Either a dictionary containing keyword arguments to be passed to the class specified via edge_type, or a dictionary whose keys are the edges, and whose values are dictionaries containing keyword arguments for the mobject related to the corresponding edge.

• partitions (list[list[Hashable]] | None) –

• root_vertex (Hashable | None) –

Examples

First, we create a small graph and demonstrate that the edges move together with the vertices.

Example: MovingVertices

from manim import *

class MovingVertices(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4]
        edges = [(1, 2), (2, 3), (3, 4), (1, 3), (1, 4)]
        g = Graph(vertices, edges)
        self.play(Create(g))
        self.wait()
        self.play(g[1].animate.move_to([1, 1, 0]),
                  g[2].animate.move_to([-1, 1, 0]),
                  g[3].animate.move_to([1, -1, 0]),
                  g[4].animate.move_to([-1, -1, 0]))
        self.wait()

class MovingVertices(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4]
        edges = [(1, 2), (2, 3), (3, 4), (1, 3), (1, 4)]
        g = Graph(vertices, edges)
        self.play(Create(g))
        self.wait()
        self.play(g[1].animate.move_to([1, 1, 0]),
                  g[2].animate.move_to([-1, 1, 0]),
                  g[3].animate.move_to([1, -1, 0]),
                  g[4].animate.move_to([-1, -1, 0]))
        self.wait()

There are several automatic positioning algorithms to choose from:

Example: GraphAutoPosition

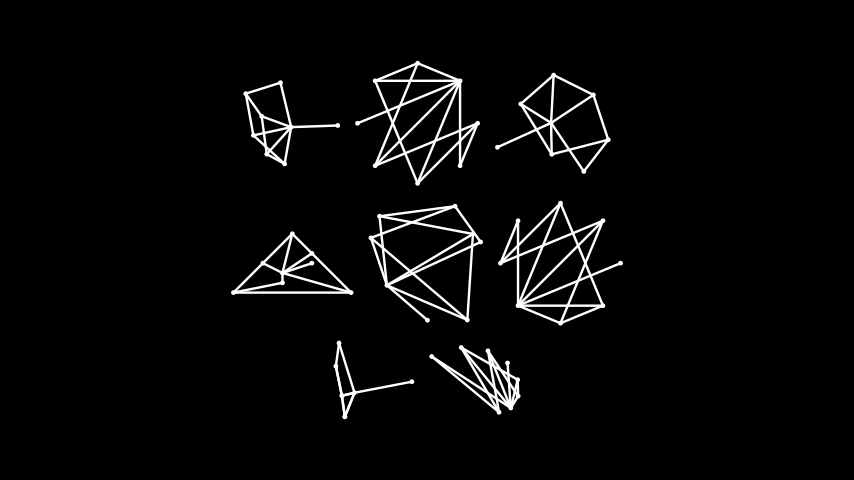
from manim import *

class GraphAutoPosition(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4, 5, 6, 7, 8]
        edges = [(1, 7), (1, 8), (2, 3), (2, 4), (2, 5),
                 (2, 8), (3, 4), (6, 1), (6, 2),
                 (6, 3), (7, 2), (7, 4)]
        autolayouts = ["spring", "circular", "kamada_kawai",
                       "planar", "random", "shell",
                       "spectral", "spiral"]
        graphs = [Graph(vertices, edges, layout=lt).scale(0.5)
                  for lt in autolayouts]
        r1 = VGroup(*graphs[:3]).arrange()
        r2 = VGroup(*graphs[3:6]).arrange()
        r3 = VGroup(*graphs[6:]).arrange()
        self.add(VGroup(r1, r2, r3).arrange(direction=DOWN))

class GraphAutoPosition(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4, 5, 6, 7, 8]
        edges = [(1, 7), (1, 8), (2, 3), (2, 4), (2, 5),
                 (2, 8), (3, 4), (6, 1), (6, 2),
                 (6, 3), (7, 2), (7, 4)]
        autolayouts = ["spring", "circular", "kamada_kawai",
                       "planar", "random", "shell",
                       "spectral", "spiral"]
        graphs = [Graph(vertices, edges, layout=lt).scale(0.5)
                  for lt in autolayouts]
        r1 = VGroup(*graphs[:3]).arrange()
        r2 = VGroup(*graphs[3:6]).arrange()
        r3 = VGroup(*graphs[6:]).arrange()
        self.add(VGroup(r1, r2, r3).arrange(direction=DOWN))

Vertices can also be positioned manually:

Example: GraphManualPosition

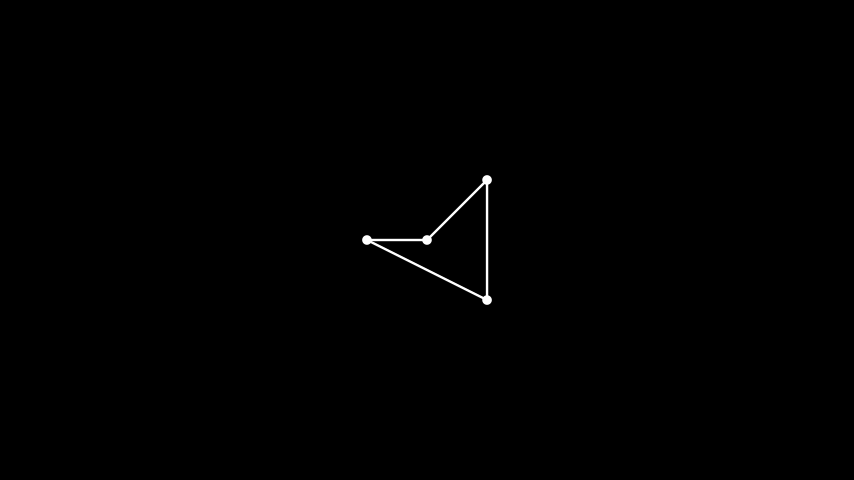
from manim import *

class GraphManualPosition(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4]
        edges = [(1, 2), (2, 3), (3, 4), (4, 1)]
        lt = {1: [0, 0, 0], 2: [1, 1, 0], 3: [1, -1, 0], 4: [-1, 0, 0]}
        G = Graph(vertices, edges, layout=lt)
        self.add(G)

class GraphManualPosition(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4]
        edges = [(1, 2), (2, 3), (3, 4), (4, 1)]
        lt = {1: [0, 0, 0], 2: [1, 1, 0], 3: [1, -1, 0], 4: [-1, 0, 0]}
        G = Graph(vertices, edges, layout=lt)
        self.add(G)

The vertices in graphs can be labeled, and configurations for vertices and edges can be modified both by default and for specific vertices and edges.

Note

In edge_config, edges can be passed in both directions: if (u, v) is an edge in the graph, both (u, v) as well as (v, u) can be used as keys in the dictionary.

Example: LabeledModifiedGraph

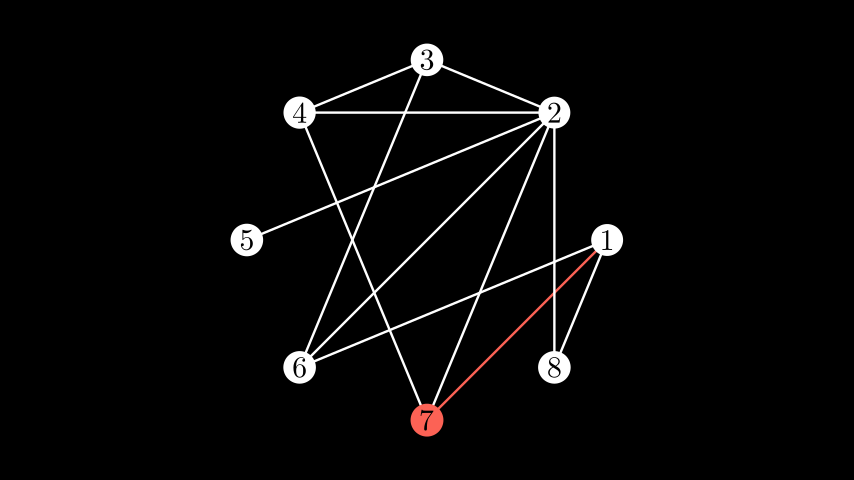
from manim import *

class LabeledModifiedGraph(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4, 5, 6, 7, 8]
        edges = [(1, 7), (1, 8), (2, 3), (2, 4), (2, 5),
                 (2, 8), (3, 4), (6, 1), (6, 2),
                 (6, 3), (7, 2), (7, 4)]
        g = Graph(vertices, edges, layout="circular", layout_scale=3,
                  labels=True, vertex_config={7: {"fill_color": RED}},
                  edge_config={(1, 7): {"stroke_color": RED},
                               (2, 7): {"stroke_color": RED},
                               (4, 7): {"stroke_color": RED}})
        self.add(g)

class LabeledModifiedGraph(Scene):
    def construct(self):
        vertices = [1, 2, 3, 4, 5, 6, 7, 8]
        edges = [(1, 7), (1, 8), (2, 3), (2, 4), (2, 5),
                 (2, 8), (3, 4), (6, 1), (6, 2),
                 (6, 3), (7, 2), (7, 4)]
        g = Graph(vertices, edges, layout="circular", layout_scale=3,
                  labels=True, vertex_config={7: {"fill_color": RED}},
                  edge_config={(1, 7): {"stroke_color": RED},
                               (2, 7): {"stroke_color": RED},
                               (4, 7): {"stroke_color": RED}})
        self.add(g)

You can also lay out a partite graph on columns by specifying a list of the vertices on each side and choosing the partite layout.

Note

All vertices in your graph which are not listed in any of the partitions are collected in their own partition and rendered in the rightmost column.

Example: PartiteGraph

from manim import *

import networkx as nx

class PartiteGraph(Scene):
    def construct(self):
        G = nx.Graph()
        G.add_nodes_from([0, 1, 2, 3])
        G.add_edges_from([(0, 2), (0,3), (1, 2)])
        graph = Graph(list(G.nodes), list(G.edges), layout="partite", partitions=[[0, 1]])
        self.play(Create(graph))

import networkx as nx

class PartiteGraph(Scene):
    def construct(self):
        G = nx.Graph()
        G.add_nodes_from([0, 1, 2, 3])
        G.add_edges_from([(0, 2), (0,3), (1, 2)])
        graph = Graph(list(G.nodes), list(G.edges), layout="partite", partitions=[[0, 1]])
        self.play(Create(graph))

The representation of a linear artificial neural network is facilitated by the use of the partite layout and defining partitions for each layer.

Example: LinearNN

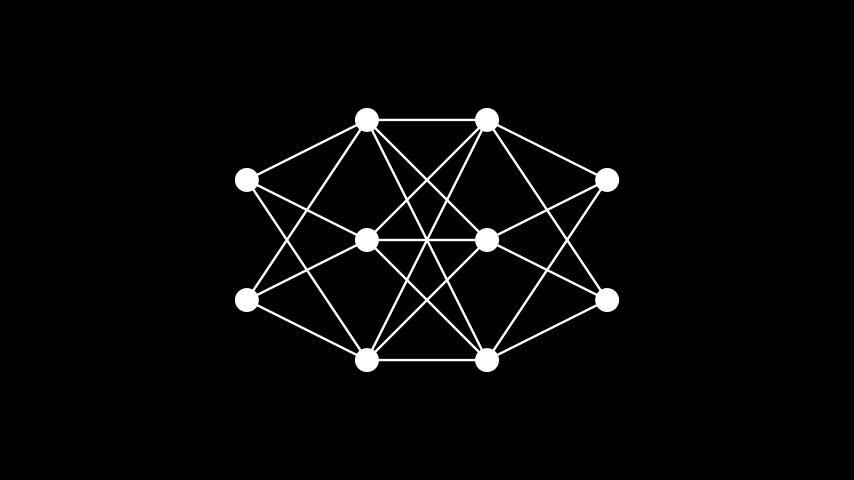
from manim import *

class LinearNN(Scene):
    def construct(self):
        edges = []
        partitions = []
        c = 0
        layers = [2, 3, 3, 2]  # the number of neurons in each layer

        for i in layers:
            partitions.append(list(range(c + 1, c + i + 1)))
            c += i
        for i, v in enumerate(layers[1:]):
                last = sum(layers[:i+1])
                for j in range(v):
                    for k in range(last - layers[i], last):
                        edges.append((k + 1, j + last + 1))

        vertices = np.arange(1, sum(layers) + 1)

        graph = Graph(
            vertices,
            edges,
            layout='partite',
            partitions=partitions,
            layout_scale=3,
            vertex_config={'radius': 0.20},
        )
        self.add(graph)

class LinearNN(Scene):
    def construct(self):
        edges = []
        partitions = []
        c = 0
        layers = [2, 3, 3, 2]  # the number of neurons in each layer

        for i in layers:
            partitions.append(list(range(c + 1, c + i + 1)))
            c += i
        for i, v in enumerate(layers[1:]):
                last = sum(layers[:i+1])
                for j in range(v):
                    for k in range(last - layers[i], last):
                        edges.append((k + 1, j + last + 1))

        vertices = np.arange(1, sum(layers) + 1)

        graph = Graph(
            vertices,
            edges,
            layout='partite',
            partitions=partitions,
            layout_scale=3,
            vertex_config={'radius': 0.20},
        )
        self.add(graph)

The custom tree layout can be used to show the graph by distance from the root vertex. You must pass the root vertex of the tree.

Example: Tree

from manim import *

import networkx as nx

class Tree(Scene):
    def construct(self):
        G = nx.Graph()

        G.add_node("ROOT")

        for i in range(5):
            G.add_node("Child_%i" % i)
            G.add_node("Grandchild_%i" % i)
            G.add_node("Greatgrandchild_%i" % i)

            G.add_edge("ROOT", "Child_%i" % i)
            G.add_edge("Child_%i" % i, "Grandchild_%i" % i)
            G.add_edge("Grandchild_%i" % i, "Greatgrandchild_%i" % i)

        self.play(Create(
            Graph(list(G.nodes), list(G.edges), layout="tree", root_vertex="ROOT")))

import networkx as nx

class Tree(Scene):
    def construct(self):
        G = nx.Graph()

        G.add_node("ROOT")

        for i in range(5):
            G.add_node("Child_%i" % i)
            G.add_node("Grandchild_%i" % i)
            G.add_node("Greatgrandchild_%i" % i)

            G.add_edge("ROOT", "Child_%i" % i)
            G.add_edge("Child_%i" % i, "Grandchild_%i" % i)
            G.add_edge("Grandchild_%i" % i, "Greatgrandchild_%i" % i)

        self.play(Create(
            Graph(list(G.nodes), list(G.edges), layout="tree", root_vertex="ROOT")))

The following code sample illustrates the use of the vertex_spacing layout parameter specific to the "tree" layout. As mentioned above, setting vertex_spacing overrides the specified value for layout_scale, and as such it is harder to control the size of the mobject. However, we can adjust the captured frame and zoom out by using a MovingCameraScene:

class LargeTreeGeneration(MovingCameraScene):
    DEPTH = 4
    CHILDREN_PER_VERTEX = 3
    LAYOUT_CONFIG = {"vertex_spacing": (0.5, 1)}
    VERTEX_CONF = {"radius": 0.25, "color": BLUE_B, "fill_opacity": 1}

    def expand_vertex(self, g, vertex_id: str, depth: int):
        new_vertices = [f"{vertex_id}/{i}" for i in range(self.CHILDREN_PER_VERTEX)]
        new_edges = [(vertex_id, child_id) for child_id in new_vertices]
        g.add_edges(
            *new_edges,
            vertex_config=self.VERTEX_CONF,
            positions={
                k: g.vertices[vertex_id].get_center() + 0.1 * DOWN for k in new_vertices
            },
        )
        if depth < self.DEPTH:
            for child_id in new_vertices:
                self.expand_vertex(g, child_id, depth + 1)

        return g

    def construct(self):
        g = Graph(["ROOT"], [], vertex_config=self.VERTEX_CONF)
        g = self.expand_vertex(g, "ROOT", 1)
        self.add(g)

        self.play(
            g.animate.change_layout(
                "tree",
                root_vertex="ROOT",
                layout_config=self.LAYOUT_CONFIG,
            )
        )
        self.play(self.camera.auto_zoom(g, margin=1), run_time=0.5)

Methods

update_edges

Attributes

animate	Used to animate the application of any method of self.
animation_overrides
color
depth	The depth of the mobject.
fill_color	If there are multiple colors (for gradient) this returns the first one
height	The height of the mobject.
n_points_per_curve
sheen_factor
stroke_color
width	The width of the mobject.

static _empty_networkx_graph()

Return an empty networkx graph for the given graph type.

Return type:

Graph

_original__init__(vertices, edges, labels=False, label_fill_color=ManimColor('#000000'), layout='spring', layout_scale=2, layout_config=None, vertex_type=<class 'manim.mobject.geometry.arc.Dot'>, vertex_config=None, vertex_mobjects=None, edge_type=<class 'manim.mobject.geometry.line.Line'>, partitions=None, root_vertex=None, edge_config=None)

Initialize self. See help(type(self)) for accurate signature.

Parameters:

• vertices (list[Hashable]) –

• edges (list[tuple[Hashable, Hashable]]) –

• labels (bool | dict) –

• label_fill_color (str) –

• layout (str | dict) –

• layout_scale (float | tuple) –

• layout_config (dict | None) –

• vertex_type (type[manim.mobject.mobject.Mobject]) –

• vertex_config (dict | None) –

• vertex_mobjects (dict | None) –

• edge_type (type[manim.mobject.mobject.Mobject]) –

• partitions (list[list[Hashable]] | None) –

• root_vertex (Optional[Hashable]) –

• edge_config (dict | None) –

Return type:

None

_populate_edge_dict(edges, edge_type)

Helper method for populating the edges of the graph.

Parameters:

• edges (list[tuple[Hashable, Hashable]]) –

• edge_type (type[manim.mobject.mobject.Mobject]) –